Question

How long does it take $1125 to triple if it is invested at 7% interest, compounded quarterly? round your answer to the nearest tenth?

Answer 1

It takes 15.83 years to triple $1125 if it is invested at 7% interest.

Explanation:

The future value (FV) of an investment of present value (PV) dollars earning interest at an annual rate of r compounded n times per year for a period of t years is:

`FV=PV(1+(r)/(n))^(nt)`

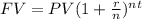
where r/n is the interest per compounding period and nt is the number of compounding periods.

We solve for t,

`PV\left(1+(r)/(n)\right)^(nt)=FV\\\\(PV\left(1+(r)/(n)\right)^(nt))/(PV)=(FV)/(PV)\\\\\left(1+(r)/(n)\right)^(nt)=(FV)/(PV)\\\\\ln \left(\left(1+(r)/(n)\right)^(nt)\right)=\ln \left((FV)/(PV)\right)\\\\nt\ln \left(1+(r)/(n)\right)=\ln \left((FV)/(PV)\right)\\\\t=(\ln \left((FV)/(PV)\right))/(n\ln \left(1+(r)/(n)\right))`

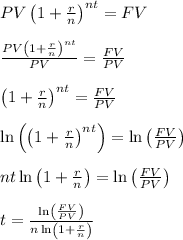
When
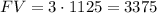`FV = 3\cdot 1125=3375`, PV = 1125, r = 7%, and n = 4, this becomes

`t=(\ln \left((3375)/(1125)\right))/(4\ln \left(1+(7/100)/(4)\right))\\\\t = (\ln \left(3\right))/(4\ln \left((407)/(400)\right))\\\\t\approx15.83`

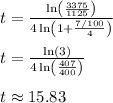
It takes 15.83 years to triple $1125 if it is invested at 7% interest.

Answer 2

To solve this problem you must apply the proccedure shown below:
1. You have to apply the following formula:
FV=PV[1+(i/n)]^4t
FV=3x1125
FV=3375
PV=1125
i=0.07
n=4
2. When you substitute the values into the formula, you obtain:
3375=1125[1+(0.07/4)]^4t
3. Now, you must solve for t, as following:
3375/1125=1+(0.07/4)^4t
3=(1.0175)^4t
log(3)=log(1.0175)^4t
log(3)=4t(log(1.0175))
4t=63.32
t=15.83 years
The answer is: 15.83 years.