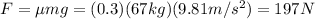The force of friction acting on Tyler is given by:
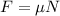
(1)
where
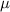
is the coefficient of friction, and N is the normal force exerted by the floor on Tyler. However, the normal force is equal to Tyler's weight:
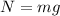
where m is Tyler's mass and g is the gravitational acceleration. Therefore, the frictional force (1) becomes