Question

What are the vertex and x-intercepts of the graph of the function given below?

y = x^2 – 2x – 48

A. Vertex: (1, –49); x-intercepts: (8, 0) and (–6, 0)
B. Vertex: (1, –40); x-intercepts: (6, 0) and (7, 0)
C. Vertex: (–1, –21); x-intercepts: (6, 0) and (4, 0)
D. Vertex: (0, 0); x-intercepts: (–4, 0) and (6, 0)

Answer 1

D. Vertex: (1, –49); x-intercepts: (8, 0) and (–6, 0)

Answer 2

VERTEX
To determine the vertex (coordinate x) of parabola y = ax² + bx + c, use this following formula
x vertex =
`-(b)/(2a)`

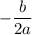
y = x² - 2x - 48
a = 1, b = -2, c = -48
plug in the numbers
x vertex =
`-(b)/(2a)`
x vertex =
`-((-2))/(2(1))`
x vertex =
`(2)/(2)`
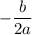
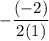
x vertex = 1

To find y vertex, substitute the value of x vertex to the parabola equation
y = x² - 2x - 48
y = 1² - 2(1) - 48
y = 1 - 2 - 48
y = -49

The vertex is (1, -49)

X-INTERCEPT
x-intercept located in x axis, that means y = 0. Substitute y = 0 to the parabola equation
x² - 2x - 48 = y
x² - 2x - 48 = 0
(x - 8)(x + 6) = 0
x = 8 or x = -6
The x-intercepts are (8,0) and (-6,0)

The answer is first option