Question

A new test to detect tb has been designed. it is estimated that 89% of people taking this test have the disease. the test detects the disease in 97% of those who have the disease. the test does not detect the disease in 99% of those who do not have the disease. if a person taking the test is chosen at random, what is the probability of the test indicating that the person does not have the disease?

Answer 1

The probability is 1 in 945 million

Answer 2

0.1356

Step-by-step explanation:

This is a probability exercise. Let's define some probability concepts.

Given two events A and B :

(A∩B) = (A,B)

(A,B) is the intersection event where A and B occur both at the same time.

We define
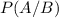`P(A/B)` as the conditional probability '' The probability of the event A given that we know that the event B occurred'' as :

`P(A/B)=(P(A,B))/(P(B))`

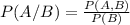
Where
`P(B)>0`

Now, if A is an event and
`A'` is its complement ⇒

`P(A)=1-P(A')`

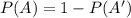
Finally we define the probability of the union between two events A and B :

P(A∪B) = P(A) + P(B) - P(A,B)

If the events A and B are independent between them ⇒ P(A,B) = 0 ⇒

P(A∪B) = P(A) + P(B)

Let's define the following events for this exercise :

D : ''People taking this test that have the disease''

`P(D)=0.89`

`P(D')=1-P(D)=1-0.89=0.11`

`P(D')=0.11`

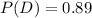
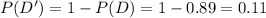
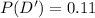
P : ''The test is positive''

`P(P/D)=0.97`

`P(P'/D)=1-P(P/D)=1-0.97=0.03`

`P(P'/D)=0.03`

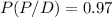
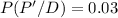
And
`P(P'/D')=0.99`

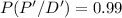
We are looking the probability of
`P(P')`

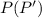
P(P') = P [(P'∩D) ∪ (P'∩D')]

Given that this events are independent between them :

`P(P')=P(P',D)+P(P',D')` (I)

Let's write the conditionals for this problem :

`P(P'/D)=(P(P',D))/(P(D))` ⇒

`P(P',D)=P(P'/D).P(D)`

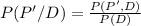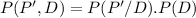
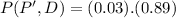`P(P',D)=(0.03).(0.89)` (II)

And the another conditional :

`P(P'/D')=(P(P',D'))/(P(D'))` ⇒

`P(P',D')=P(P'/D').P(D')`

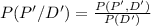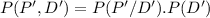
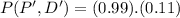`P(P',D')=(0.99).(0.11)` (III)

Replacing (II) and (III) in (I) :

`P(P')=(0.03).(0.89)+(0.99).(0.11)`

`P(P')=0.1356`

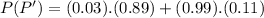
We find that the probability of the test indicating that the person does not have the disease ( P(P') ) is 0.1356