Question

Using the transformation T : (x, y) → (x + 2, y + 1), find the distance named. Round the distance to the nearest hundredth of a unit. Complete your work in the space provided or upload a file that can display math symbols if your work requires it.

Find the distance C'A'.

Answer 1

C' is located at (0, 3) and A' is located at (2, 1).

d=√(x₂-x₁)²+(y₂-y₁)²
d=√(2-0)²+(1-3)²
d=√(2)²+(-2)²
d=√4+4
d=√8
d=2.83

The distance between points C' and A' is 2.83 units.

Answer 2

The distance C'A' is
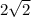`2√(2)` units.

Explanation:

From the given graph it is clear that the coordinates of C' and A' are C'(0,3) and A'(2,1).

Distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

Using distance formula, the distance between C' and A' is

`C'A'=√((2-0)^2+(1-3)^2)`

On simplification we get

`C'A'=√((2)^2+(-2)^2)`

`C'A'=√(4+4)`

`C'A'=√(8)`

`C'A'=2√(2)`

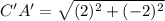
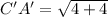
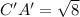
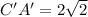
Therefore the distance C'A' is
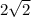`2√(2)` units.