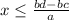Question

Please help! Math question.

Answer 1

It’s it’s the fits the first one

Answer 2

When solving inequalities, you can treat it like you would an equation with an equal sign. However, remember that whenever you multiply or divide by a negative number, you must flip the inequality sign.

You're given
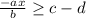
`(-ax)/(b) \geq c -d` and asked to solve for x:
1) Multiply both sides by b

`(-ax)/(b) \geq c -d \\ -ax \geq b(c-d)`

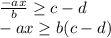
2) Distribute the b to the c and d using the distributive property

`-ax \geq b(c-d)\\ -ax \geq b(c)-b(d)\\ -ax \geq bc-bd`

3) Divide both sides by -a. Don't forget to flip the inequality sign!

`-ax \geq bc-bd\\ x \leq (bc-bd)/(-a)`

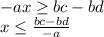
4) Simplify by multiplying the right side by
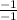`(-1)/(-1)` (aka 1) to get rid of the negative on the a. You don't need to flip the sign here (think of it as dividing and the multiplying by -1, so you flip it twice, which is the same as not flipping at all!)

`x \leq (bc-bd)/(-a) \\ x \leq (bc-bd)/(-a) ( (-1)/(-1) )\\ x \leq (-bc+bd)/(a) \\ x \leq (bd-bc)/(a)`

------

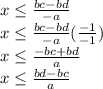
Answer: Top right,
`x \leq (bd-bc)/(a)`