Question 3 ⇒⇒ one part
The upper shaded figure represents rhombus
So, the angles 60° and (5x + 15)° are supplementary
∴ 60° + (5x + 15)° = 180°
Solve for x
∴ 5x + 75 = 180
∴ 5x = 180 - 75 = 105
∴ x = 105/5 = 21
So, the value of x = 21===================================================
Question 4 ⇒⇒ two partswe will use the following sequence to find the area of each triangle
1. calculating the length of each side using the distance between two points (x₁,y₁),(x₂,y₂) = d
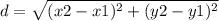
2. calculating the area using Heron's Formula
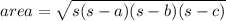
where a, b and c are the lengths of sides of the triangle
and s is the half of the triangles perimeter = (a+b+c)/2
Part (1): The area of RST
R(-5,-5) , S(-3,-1) , T(-1,-2)
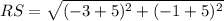 = √20
= √20
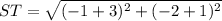 = √5
= √5
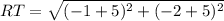 = 5
= 5
s = (√20 + √5 + 5)/2 ≈ 5.85
∴ Area =
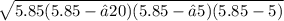 = 5
= 5
∴ Area of ΔRST = 5
Part (2): The area of MNLM(1,0) , N(3,2) , L(4,-2)
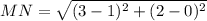 = 2√2
= 2√2
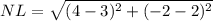 = √17
= √17

= √13
s = (2√2 + √17+ √13)/2 ≈ 5.28
∴ Area =
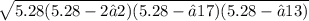
= 5
∴ Area of ΔMNL = 5
====================================================
Question 8 ⇒⇒ four parts Part (1)⇒⇒⇒ A. hexagonal prism
Part (2)⇒⇒⇒ B. rectangular pyramid
Part (3)⇒⇒⇒ C. triangular prism
Part (4)⇒⇒⇒ D. triangular pyramid
The complete answer is as shown in the attached figure