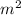Question

Help me find the area of the rhombus

Answer 1

area of a rhombus is bxh
5x10=50m^2

Answer 2

The equation for the area of a rhombus is
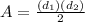
`A = ( (d_1)( d_2))/(2)`, where
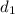
`d_1` and
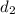
`d_2` are the length of the diagonals of the rhombus, and A = area of the rhombus.

Your two diagonals are:

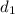
`d_1` = 5m + 5m = 10m

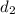
`d_2` = 10m + 10m = 20m

Plug these values into the equation for the area of a rhombus:

`A = ( (d_1)( d_2))/(2) \\ A = ( (10)(20))/(2) \\ A = (200)/(2) \\ A = 100m^2`

-----

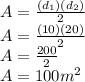
Answer: 100
`m^(2)`