Question

The price that a company charged for a basketball hoop is given by the equation 50 - 5x^2 where x is the number of hoops that are produced, in millions. It costs the company $30 to make each basketball hoop. The company recently reduced its production to 1 million hoops but maintained its profit of 15 million dollars. Approximately how many basketball hoops did the company previously produce to make the same profit?

1.3 million hoops
1.4 million hoops
15 million hoops
30 million hoops

Answer 1

A!!!!!

Step-by-step explanation:

Answer 2

Answer: The correct option is first, the number of basketball hoops did the company previously produce to make the same profit is 1.3 million hoops.

Step-by-step explanation:

Let the number of basketball hoops did the company previously produce to make the same profit be x.

Total Revenue = Price * Quantity

The total revenue in million dollars is,

`\text{Total Revenue}=(50-5x^2)x`

`\text{Total Revenue}=50x-5x^3`

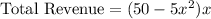
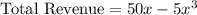
The total cost in million dollars is,

Total Cost = One unit cost * Quantity

`\text{Total Cost}=30x`

Profit = Total Revenue - Total Cost

`\text{Profit}=50x-5x^3-30x`

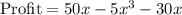
The profit is 15 million.

`15=20x-5x^3`

`5x^3-20x+15=0\\x^2-4x+3=0\\(x-1)(x^2+x-3)=0`

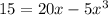
The value of x is 1 and
`(-1\pm √(13))/(2)`.

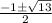The production is always positive therefore the value of x either 1 or 1.3. Since 1 million is not available in the options therefore the the correct optin is 1.3 million hoops.