Question

What function is represented below?

f(x) = (1/4)^x+2
f(x) = (1/4)^x +2
f(x) = (1/4)^x-2
f(x) = (1/4)^x -2

Answer 1

The correct option is 3, i.e.,
`f(x)=((1)/(4))^(x-2)`.

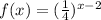Explanation:

From the graph it is clear that as x tends to infinity, then the value of function tends to 0 and y-intercept of the function is at above (0,8).

In option 1:

`f(x)=((1)/(4))^(x+2)`

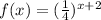
At x=0,

`f(0)=((1)/(4))^(0+2)=0.063`

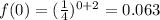
The y-intercept of this function is 0.063, which is less than 8, therefore option 1 is incorrect.

In option 2:

`f(x)=((1)/(4))^(x)+2`

At x=0,

`f(0)=((1)/(4))^(0)+2=3`

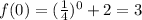
The y-intercept of this function is 3, which is less than 8, therefore option 2 is incorrect.

In option 3:

`f(x)=((1)/(4))^(x-2)`

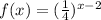
At x=0,

`f(0)=((1)/(4))^(0-2)=16`

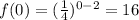
The y-intercept of this function is 16, which is more than 8, therefore option 3 is correct.

In option 4:

`f(x)=((1)/(4))^(x)-2`

At x=0,

`f(0)=((1)/(4))^(0)-2=-1`

The y-intercept of this function is -1, which is less than 8, therefore option 4 is incorrect.

Answer 2

By graphing the given options as shown in attached figure
f(x) = (1/4)^x+2 ⇒⇒⇒⇒ The black graph
f(x) = (1/4)^x +2 ⇒⇒⇒⇒ The red graph
f(x) = (1/4)^x-2 ⇒⇒⇒⇒ The blue graph
f(x) = (1/4)^x -2 ⇒⇒⇒⇒ The green graph


The correct answer will be the blue graph


`f(x) = ((1)/(4))^((x-2))`