Question

Given the equation Square root of 2x plus 1 = 3, solve for x and identify if it is an extraneous solution. x = 4, solution is extraneous x = 4, solution is not extraneous x = 5, solution is extraneous x = 5, solution is not extraneous

Answer 1

`\text{The domain:}\\2x+1\geq0\to 2x\geq-1\to x\geq-0.5\\\\D:x\geq0.5\to x\in\left\ \textless \ 0.5;\ \infty\right)\\\\√(2x+1)=3\ \ \ \ |\text{square both sides} \\2x+1=3^2\\2x+1=9\ \ \ |-1\\2x=8\ \ \ \ |:2\\x=4\in D\\\\\text{Answer: x =0, solution is not extraneous}.`

Answer 2

Answer: The correct option is

(B) solution is x = 4, the solution is not extraneous.

Step-by-step explanation: We are given to solve the following equation :

`√(2x+1)=3~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

And, we are to select the correct option about the solution of the above equation.

From equation (i), we have

`√(2x+1)=3\\\\\Rightarrow 2x+1=3^2~~~~~~~~~~~~~~[\textup{Squaring both sides}]\\\\\Rightarrow 2x+1=9\\\\\Rightarrow 2x=9-1\\\\\Rightarrow 2x=8\\\\\Rightarrow x=(8)/(2)\\\\\Rightarrow x=4.`

So, x = 4 is a solution of the given equation.

Now, substituting x = 4 in the left hand side of equation (i), we get

`L.H.S.=√(2*4+1)=√(8+1)=√(9)=3=R.H.S.`

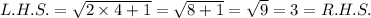
Since x = 4 satisfy the given equation, so it is not an extraneous solution.

Thus, the required solution is x = 4, the solution is not extraneous.

Option (B) is CORRECT.