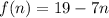Question

Find an explicit formula for the arithmetic sequence 12, 5, -2, -9..

Answer 1

T(n)=19-7n
You can use this formula to check if I’m right or wrong by plugging the term # for n...it will show you the # of the term

Answer 2

Answer:
`f(n)=19-7n`

Explanation:

The explicit formula for an arithmetic sequence is given by :-

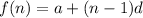`f(n)=a+(n-1)d` (1)

, where a = first term

d= common difference

n= number of term

The given arithmetic sequence = 12, 5, -2, -9..

First term : a = 12

Common difference : d= 5-12=-7 [Difference between any two consecutive terms.]

Put a = 12 and d= -7 in (1) , we get

`f(n)=12+(n-1)(-7)`

Hence, the explicit formula for the given arithmetic sequence :
`f(n)=12+(n-1)(-7)`

We we solve it further , we get

`f(n)=12-7n+7`

`f(n)=19-7n`

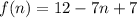
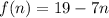
Required explicit formula :
`f(n)=19-7n`