Question

Help me please!!!!!!!!!!!

Answer 1

The difference in area is pi*(6^2-3^2), or pi(36-9), or pi(27). This is approx. 84.82 square inches.

Price per square inch: small pizza: $3.50 / [pi*3^2] = $0.124 / square inch
large pizza: $11 / [pi*6^2] = $0.097 / sq. inch

Thus, the larger pizza is the better deal; its cost per square inch is the lesser.

Answer 2

a.

Area of a circle is
`A= \pi r ^(2)`

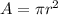
And to get the radius, you'll need to divide the diameter, 6 and 12, by half. So in this case the radiuses are 3 and 6.

6-inch pizza:

`A= \pi 3^2 \\ A=9 \pi \\ A=28.27`

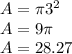
12-inch pizza:

`A= \pi 6^(2) \\ A= 36 \pi \\ A=113.10`

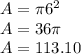
Now to just subtract the areas:
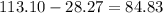
`113.10-28.27=84.83` . There is 84.83 less area on the 6-inch compared to the 12-inch.


b.

So the best way to find what is the better deal is to find the unit price. For the numerator i'll be doing the price of the pizzas and the denominator will be the area of the pizzas. Then i'll be dividing those fractions by the denominator and the better deal is going to be the answer with the smaller unit price.

6-inch pizza:
`(3.50)/(28.27) / (28.27)/(28.27) = (0.12)/(1)`

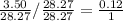
12-inch pizza:
`(11)/(113.10) / (113.10)/(113.10) = (0.10)/(1)`

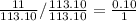
The 12-inch pizza is the better deal because you pay only 10 cents per singular area vs the 6-inch pizza which costs 12 cents per singular area.