Group your x stuff together and your y stuff together and move the constant over to the other side to start.
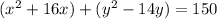
. Now complete the squares on the x and y terms by taking half the linear terms (the x and y terms), squaring it, and then adding it to both sides. In the set of parenthesis with the x, the linear term is 16. Half of 16 is 8 and 8 squared is 64, so add it to both sides. Now for the y terms. In the set of parenthesis with the y, the linear term is 14. Half of 14 is 7 and 7 squared is 49. So add that in too. Now what you have is this:
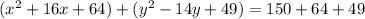
Simplifying that down into its perfect square binomials you have the equation for the circle now:
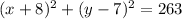
. The center then is (-8, 7)