Okay, haven't done physics in years, let's see if I remember this.
So Coulomb's Law states that
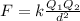
so if we double the charge on

and double the distance to
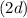
we plug these into the equation to find
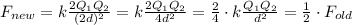
So we see the new force is exactly 1/2 of the old force so your answer should be
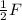 if I can remember my physics correctly.
if I can remember my physics correctly.