Question

Ramone has 5 difficult questions left to answer on a multiple choice test. Unfortunately, he is running out of time and must guess for the remaining questions. Each question has 3 choices. For the first 2 of these questions, he eliminated 1 of the 3 choices. Find the probability that he will answer the first 2 questions, as well as at least 2 of the 3 remaining questions correctly.

Answer 1

i belive it will be 4 out of 8

Answer 2

Question #1: He eliminated 1 of the 3 choices. So the probability of getting correct answer is 1/2.

Question #2: He eliminated 1 of the 3 choices. So the probability of getting correct answer is 1/2.

For Question #3-5: The probability of getting correct answer is 1/3 and getting incorrect it 2/3.

He should get at least 2 out of 3 correctly answered. The probability would be :-

P(at least 2 correct out of 3) = P(exactly 2 correct) + P(all 3 correct)

`Probability=C(3,2)*((1)/(3) )^(2) *((2)/(3) ) + C(3,3)*((1)/(3) )^(3) \\\\ Probability=3*((1)/(9)) *((2)/(3) ) + 1*((1)/(27) ) \\\\ Probability=(6)/(27)+(1)/(27) \\\\ Probability=(6+1)/(27)=(7)/(27)`

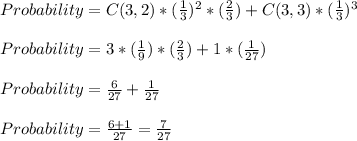
Combined probability would be =
`(1)/(2) *(1)/(2)* (7)/(27) =(7)/(108)`