From trigonometry we know that:
if

then,
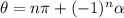 (where
(where
 is an integer)
is an integer)
This can be rewritten in degrees as:
 .............(Equation 1)
.............(Equation 1)
Now, in our case,
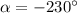
Therefore, (Equation 1) can be written as:
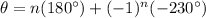 ..........(Equation 2)
..........(Equation 2)
Now, to find the correct options all that we have to do is replace n by relevant integers and find the values of
 that match.
that match.
For n=2, (Equation 2) gives us:
 .
.
Thus,

Now, we know that:

Let n=-1, then:
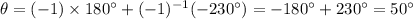
Thus,
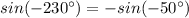
Likewise,
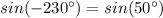
Only the last option
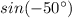 will never match
will never match
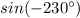 because no integral value of
because no integral value of
 will ever give
will ever give

Thus the last option is the correct option.