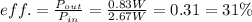Question

A winch system powered by a 7.2 volt motor is used to lift a 30 Newton load a distance of 2.5 meters. The motor's current rating is 370 milliamps. What is the efficiency of the electro-mechanical system if the time required to raise the load is 90 seconds?

Answer 1

The power transferred by the motor is equal to the product between the current and the voltage:

`P_(in)=VI=(7.2 V)(0.37 A)=2.67 W`

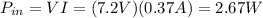
However, the power used by the winch system is less than this value. In fact, the work done is equal to the weight of the load times the distance through which it has been lifted:

`W=Fd=(30 N)(2.5 m)=75 J`
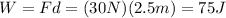
And the power used by the system is the work done divided by the time taken:

`P_(out)= (W)/(t)= (75 J)/(90 s)=0.83 W`

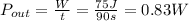
Therefore, the efficiency of the system is given by the ratio between the useful power and the power in input:

`eff.= (P_(out))/(P_(in))= (0.83 W)/(2.67 W)=0.31 = 31\%`