Question

A house cost $120,000 when it was purchased. The value of the house increases by 10% each year. Find the rate of growth each month and select the correct answer below.

Answer 1

The house cost = $120,000
The value of the house increases by 10% each year
While the year = 12 months

The value of the house increases by 10% over 12 each month =
`(10)/(12) \%`

∴ The rate of growth each month =
`(10)/(12) \% * 120,000 = (10)/(12) * (1)/(100) * 120,000 = 1,000`

So, the correct answer is
`(10)/(12) \%` = $1,000 each month

Answer 2

The growth rate for each month is
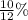`(10)/(12)\%` or 0.833%.

Explanation:

It is given that the initial cost of house is $120,000.

The value of the house increases by 10% each year.

It means the growth rate is 10% per year.

The growth model is defined as

`P=P_0(1+r)^t`

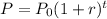
Where, P₀ is initial value, r is growth rate and t is time.

The growth model for given problem is

`P=120000(1+0.1)^t`

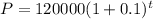
We know that

`1\text{ year}=12\text{ months}`

`1\text{ year}=10\%`

`12\text{ months}=10\%`

`1\text{ months}=(10)/(12)\%`

`1\text{ months}=0.833\%`

`120,000* (10)/(12)* (1)/(100)=1000`

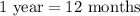
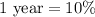
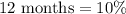
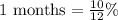
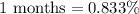
The value of house increased by $1000 per month.

Therefore growth rate for each month is
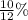`(10)/(12)\%` or 0.833%.