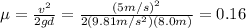Question

A shuffleboard puck having an initial speed of 5 m/s slides 8.0 m before coming to rest. what is the coefficient of kinetic friction between the puck and the surface?

Answer 1

The puck comes to rest due to the work done by the frictional force against the motion of the puck. We can solve the problem by using the work-energy theorem, which states that the work done by the frictional force is equal to the variation of kinetic energy of the puck:

`W=K_f-K_i`
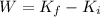
where
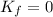
`K_f=0` is the final kinetic energy of the puck (which is zero, since the final velocity of the puck is zero), and

`K_i= (1)/(2)mv^2`
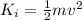
is the initial kinetic energy of the puck, with m being the mass of the puck and v its initial velocity.

We can also rewrite the work done as the product between the frictional force and the distance covered by the puck

`W=-\mu mg d`
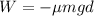
where
`\mu` is the coefficienct of kinetic friction, and where the negative sign is due to the fact that the frictional force acts against the direction of the motion. By combining the three equations together, we get

`\mu g d = (1)/(2)v^2`
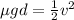
from which we can find the coefficient of kinetic friction:

`\mu = (v^2)/(2gd)= ((5 m/s)^2)/(2(9.81 m/s^2)(8.0 m))=0.16`