The electrical force between two protons is given by:
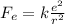
where
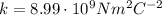
is the Coulomb's constant
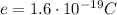
is the proton charge
r is the separation between the two protons
The gravitational force between the two protons is given by:

where
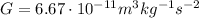
is the gravitational constant
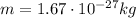
is the proton mass
r is the separation between the two protons
If we divide the electric force by the gravitational force, we get
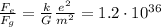
which means that the electric force between the two protons is
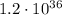
times greater than the gravitational force.
Moreover, the two protons have same electric charge, and the electrostatic force between two same-sign charges is repulsive, while the gravitational force is always attractive: therefore, the correct answer is
The electrical force is 1.2 × 1036 times greater than the gravitational force, but only the gravitational force is attractive.