Question

How many solutions does the following system have? y=x-2 -x+y=-5

no solutions
infinitely many solutions
two solutions
one solution

Answer 1

the answer is "no solutions"

Answer 2

To find how many solution our system has, we are going to find the slope of each equation.

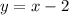
`y=x-2` equation (1)

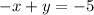
`-x+y=-5` equation (2)
To find the slope, we are going to express both equations in the form:
`y=mx+b`
where

`m` is the slope

Notice that equation (1) is already in the form
`y=mx+b`; from equation (1) we can infer that
`m=1`

To express equation (2) in the form
`y=mx+b`, we are going to add
`x` to both sides of the equation:

`-x+x+y=x-5`

`y=x+5`
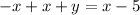
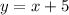
Now, we can infer that the slope of equation (2) is
`m=1`. Since both equations have the same slope, we are dealing with parallel lines; parallel lines don't intercept, so the system has no solutions.

We can conclude that the correct answer is the first choice: no solutions