Question

20 POINTS PLEAE HELP!!!!!!!!!!!!!!!

John has taken out a loan for college. He started paying off the loan with a first payment of $100. Each month he pays, he wants to pay back 1.1 times as the amount he paid the month before. Explain to John how to represent his first 20 payments in sigma notation. Then explain how to find the sum of his first 20 payments, using complete sentences. Explain why this series is convergent or divergent.

Answer 1

his first payment is $100, thus a₁ = 100.

the next "term", month will be 1.1 times more than the one before, namely r = 1.1, the common ratio.


`\bf \qquad \qquad \textit{sum of a finite geometric sequence} \\\\ S_n=\sum\limits_(i=1)^(n)\ a_1\cdot r^(i-1)\implies S_n=a_1\left( \cfrac{1-r^n}{1-r} \right)\quad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ r=\textit{common ratio}\\ ----------\\ a_1=100\\ r=1.1\\ n=20 \end{cases}`


`\bf \sum\limits_(i=1)^(20)~100(1.1)^(i-1)\qquad \qquad\qquad \qquad S_(20)=100\left( \cfrac{1-1.1^(20)}{1-1.1} \right) \\\\\\ S_(20)=100\left( \cfrac{1-\stackrel{\approx}{6.727499949}}{-0.1} \right)\implies S_(20)\approx 100(57.27499949) \\\\\\ S_(20)\approx 5727.4999493256`

is the serie divergent or convergent?

well, to make it short, when the common ratio is 0 < | r | < 1, namely a fraction between 0 and 1, only then the serie is convergent, namely it reaches a fixed value, now in this case, 1.1 is a value larger than anything between 0 and 1, so no dice.

Answer 2

The easiest way to get the answer is to use a spreadsheet. That will allow you to look at ways of getting the answer if you are not certain.

Step One
This is an exponential function and as such you have to make a built in correction factor. To get tn you need to use
tn = 100* [(1.1)^(1/20) ] ^ (20*(n - 1) )
1.1^(1/20) = 1.004776882
tn = 100 * (1.004776882)^(20*(n - 1) ) So if you want the 18th term, you do it like this.
t18 = 100*(1.004776882)^(20*(18 - 1))
t18 = 100*(1.004776882)^ 340
t18 = 100 * 5.0545
t18 = 505.45 Does that agree with what the spreadsheet gives? Amazingly enough it does!

Now we have to figure out how to get the sum of all those terms.
Oddly, you go back to 1.1


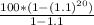
`(100*(1 - (1.1)^(20)))/(1 - 1.1)` The answer can be made closer by using the adjustment we used for each term, but as you can see, the sum is within pennies of agreement.

I don't know how to represent this using sigma notation. I could if I knew the latex for it.

It is definitely a divergent series.