Question

Solve the system of equations.

10x+y=−20

y=2x2−4x−16

( , ) and ( , )

Answer 1

I will go about solving this using the elimination method.

First, convert the equations.

10x + y = -20
4x + y = -12

Second, find the easiest variable to get rid of and get rid of it! (In this case, y) We will subtract to get rid of y.

6x = -8

Third, you want to solve the equation.

6x = -8 (divide by 6)
x =
`-1 (1)/(3)`

Fourth, solve for y by inserting the answer for x into one of the equations.

10(
`-1 (1)/(3)`) + y = -20

`-13 (1)/(3)` + y = -20 (subtract
`-13 (1)/(3)`)
y =
`-6 (2)/(3)`

The solution for this system of equations is (
`-1 (1)/(3)`,
`-6 (2)/(3)`).

Answer 2

`(-2,0)` and
`(-1,-10)`.

Explanation:

We have been given a system of equations. We are asked to solve our given system of equations.

`10x+y=-20...(1)`

`y=2x^2-4x-16...(1)`

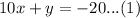
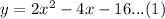
We will use substitution method to solve our given system. From equation (1) we will get,

`y=-20-10x`

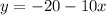
Substituting this value in equation (1) we will get,

`-20-10x=2x^2-4x-16`

`-20+20-10x=2x^2-4x-16+20`

`-10x=2x^2-4x+4`

`-10x+10x=2x^2-4x+10x+4`

`0=2x^2+6x+4`

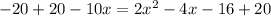
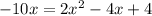
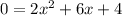
Now we will use quadratic formula to solve for x.

`x=(-b\pm √(b^2-4ac))/(2a)`

`x=(-6\pm √(6^2-4*2*4))/(2*2)`

`x=(-6\pm √(36-32))/(4)`

`x=(-6\pm √(4))/(4)`

`x=(-6)/(4)\pm (√(4))/(4)`

`x=-1.5\pm (2)/(4)`

`x=-1.5\pm 0.5`

`x=-1.5-0.5\text{ or }-1.5+0.5`

`x=-2\text{ or }-1`

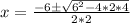
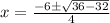
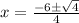
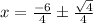
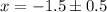
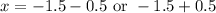
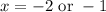
Now to find y values we will substitute
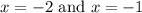`x=-2\text{ and }x=-1` in equation (1) as.

`10(-2)+y=-20`

`-20+y=-20`

`-20+20+y=-20+20`

`y=0`

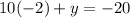
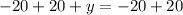
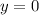
Now, we will substitute
`x=-1` in equation (1) as.

`10(-1)+y=-20`

`-10+y=-20`

`-10+10+y=-20+10`

`y=-10`

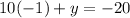
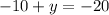
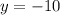
Therefore, there are two solutions for our given system that are
`(-2,0)` and
`(-1,-10)`.