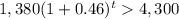Answer:
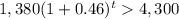
Explanation:
The exponential growth function is given by :-
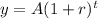 , where A is the initial value , r is the rate of growth and t is time.
, where A is the initial value , r is the rate of growth and t is time.
Given : The number of cars that passed through a tollbooth prior to 6 a.m. is 1,380.
i.e. A = 1,380
The number of cars that pass through the tollbooth from 6 a.m. through the morning rush hour increases by 46% every hour.
i.e. r=46%=0.46
Now, the function to determine the number of hours, t, after 6 a.m. when the number of cars that have passed through the tollbooth :-
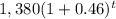
For number of cars that have passed through the tollbooth is over 4,300, we have
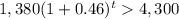
hence, the required inequality :