Question

Suppose a laboratory has a 38 g sample of polonium-210. The half-life of polonium-210 is about 138 days. How many half-lives of polonium-210 occur in 1104 days? How much polonium is in the sample 1104 days later?

9 ; 0.07 g
8 ; 2,2622 g
8 ; 4.75 g
8 ; 0.15 g

Answer 1

D. 8; 0.15 g

Explanation:

We have been given that a a laboratory has a 38 g sample of polonium-210. The half-life of polonium-210 is about 138 days.

To find the half-lives of polonium-210, we will divide 1104 by 138.

`\text{Number of half lives}=\frac{\text{Total days}}{\text{Half-life}}`

`\text{Number of half lives}=(1104)/(138)`

`\text{Number of half lives}=8`

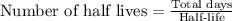
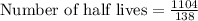
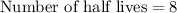
Therefore, there are 8 half-lives will occur in 1104 days.

`A=a\cdot ((1)/(2))^{(t)/(h)}`

`A=38\text{ g}\cdot (0.5)^{(1104)/(138)}`

`A=38\text{ g}\cdot (0.5)^(8)`

`A=38\text{ g}\cdot 0.00390625`

`A=0.1484375\text{ g}`

`A\approx 0.15\text{ g}`

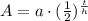
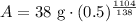
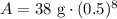
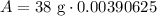
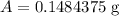
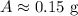
Therefore, 0.15 gm of the polonium will be left after 1104 days.

Answer 2

To find the number of half lives divide the total number of days by the number of days for 1 half live:

1104 / 138 = 8

There are 8 half lives.

To find the total amount left multiply the starting amount by 1/2 to the 8th power:

38 * 0.5^8 = 0.148 = 0.15 grams

The answer is the last one.