Question

Two people are standing on opposite sides of a hill. Person A makes an angle of elevation of 65° with the top of the hill and person B makes an angle of elevation of 80° with the top of the hill. The two people are standing 45 feet from each other.

Answer 1

71

Explanation:

Answer 2

The rest of the question is as following
What is the distance from person B to the top of the hill?
===================================================
Answer;
The attached figure represents the explanation of the problem.
So, it is required to find the distance BH
It will be calculated as following
∠A = 65° and ∠B = 80°
∴ ∠H = 180° - (65° + 80° ) = 35°
But the side AB = 45
So, we can use the sine rule to find the side BH

`(AB)/(sin \ H) = (BH)/(sin \ A)`

`BH = (sin \ A)/(sin \ H) * AB`

`BH = (sin \ 65)/(sin \ 35) * 45`

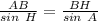
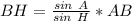
∴ BH ≈ 71.1 feet

∴ The distance from person B to the top of the hill ≈ 71.1 feet