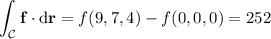Computing the line integral directly would be easy enough, but in general it's worth checking to see if the vector field is conservative; that is, whether there exists a scalar function

whose gradient corresponds exactly to the given vector field

, or
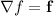
. Equivalently, we're looking for

such that
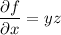
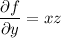
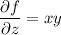
We find that
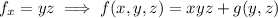
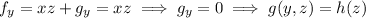
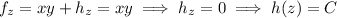
and so there is indeed such a function

, with
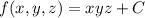
.
Thus by the fundamental theorem of calculus, the line integral is path-independent, and
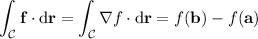
where
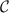
is any path starting at
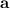
and ending at
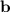
. Here,