Question

G find the domain for the particular solution to the differential equation dy dx equals the quotient of negative 1 times x and y, with initial condition y(2) = 2.

Answer 1

`(dy)/(dx) = (-x)/(y)`
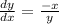
by separating the variables
∴ y dy = -x dx
integrating both sides with respect to x
∴ ∫y dy = ∫-x dx
∴
`( y^(2) )/(2) = - ( x^(2) )/(2) +c`
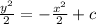
finding c using initial condition y(2) = 2.
∴
`( 2^(2) )/(2) = - ( 2^(2) )/(2) +c`
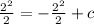
∴ c = 4
∴
`( y^(2) )/(2) = - ( x^(2) )/(2) +4`
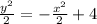
multiplying all the equation by 2
∴ y² = -x² + 8
∴ x² + y² = 8
The resultant equation represents the equation of the circle
with center (0,0) and radius = √8 = 2√2
so, the domain of this function is [-2√2 , 2√2]
See the attached figure