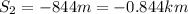Question

In reaching her destination, a backpacker walks with an average velocity of 1.41 m/s, due west. This average velocity results, because she hikes for 6.30 km with an average velocity of 2.49 m/s due west, turns around, and hikes with an average velocity of 0.630 m/s due east. How far east did she walk (in kilometers)?

Answer 1

The total average velocity
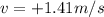
`v=+1.41 m/s` (I assume west as positive direction) is given by the total displacement, S, divided by the total time taken, t:

`v= (S)/(t)= (S_1+S_2)/(t_1+t_2)`
where:
-The total displacement S is the algebraic sum of the displacement in the first part of the motion (
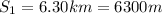
`S_1=6.30 km=6300 m`, due west) and of the displacement in the second part of the motion (
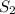
`S_2`, due east).
-The total time taken t is the time taken for the first part of the motion,
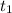
`t_1`, and the time taken for the second part of the motion,
`t_2`.
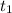
`t_1` can be found by using the average velocity and the displacement of the first part:

`t_1= (S_1)/(v_1)= (6300 m)/(2.49 m/s)=2530 s`


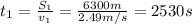
`t_2`, instead, can be written as
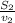
`(S_2)/(v_2)`, where
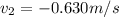
`v_2=-0.630 m/s` is the average velocity of the second part of the motion (with a negative sign, since it is due east).

Therefore, we can rewrite the initial equation as:

`v=1.41 = (6300+S_2)/(2530- (S_2)/(0.630) )`
And by solving it, we find the displacement in the second part of the motion (i.e. how far did the backpacker move east):

`S_2=-844 m=-0.844 km`