Question

A rhinoceros is at the origin of coordinates at time t1 = 0. for the time interval from t1 = 0 to t2 = 21.5 s, the rhino's average velocity has x-component -3.8 m/s and y-component 4.5 m/s. (a) at time t2 = 21.5 s, what are the x and y coordinates of the rhino? (b) how far is the rhino from the origin? ans:- -81.7 m, 96.8 m. 127m,

Answer 1

The x and y coordinates of the rhinoceros at time t2 = 21.5 s are -81.7 m and 96.8 m, respectively. The rhinoceros is approximately 127 m away from the origin at time t2 = 21.5 s.

Step-by-step explanation:

To determine the x and y coordinates of the rhinoceros at time t2 = 21.5 s, we need to use the average velocity and the time interval. The x-component of the average velocity is -3.8 m/s and the y-component is 4.5 m/s. We can calculate the change in x-coordinate by multiplying the x-component by the time interval: -3.8 m/s * 21.5 s = -81.7 m. Similarly, we can calculate the change in y-coordinate: 4.5 m/s * 21.5 s = 96.8 m. Therefore, at time t2 = 21.5 s, the x-coordinate is -81.7 m and the y-coordinate is 96.8 m.

To find the distance from the origin, we can use the Pythagorean theorem. The distance is the square root of the sum of the squares of the x and y coordinates: sqrt((-81.7)^2 + 96.8^2) = 127 m. So, the rhinoceros is approximately 127 m away from the origin at time t2 = 21.5 s.

Answer 2

a) The rhino's average velocity on the x-axis is
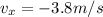
`v_x=-3.8 m/s`. The position x after time t=21.5 s can be found by using the relationship:

`x=x_0 + v_x t=0+(-3.8 m/s)(21.5 s)=-81.7 m`
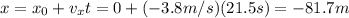
where we used
`x_0=0` as the x-position at time t=0, since the rhino was at the origin.

SImilarly, the average velocity on the y-axis is
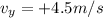
`v_y=+4.5 m/s`, and the y-position after time t=21.5 s can be found by using:

`y=y_0+(+4.5 m/s)(21.5 s)=+96.8 m`
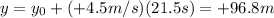
where we used
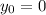
`y_0=0` since the the rhino was at the origin at time t=0.

b) The distance of the rhino from the origin can be calculated by calculating the resultant of the displacement of the rhino on both axes:

`d= √(x^2+y^2)= √((-81.7 m)^2+(96.8m)^2)=126.7 m`