Question

Calculate the work done by a 6.0-v battery as it charges a 7.6-μf capacitor in the flash unit of a camera.

Answer 1

The work done by a 6.0-V battery in charging a 7.6-μF capacitor in a camera flash unit is 136.8 microjoules.

Step-by-step explanation:

Work Done by a Battery in Charging a Capacitor

To calculate the work done by a 6.0-V battery in charging a 7.6-μF capacitor, we can use the formula:

Work = 0.5 * C * (V^2)

Where:
C is the capacitance of the capacitor (in farads) = 7.6 × 10^-6 F
V is the voltage across the capacitor = 6.0 V

Plugging in the values:
Work = 0.5 * 7.6 × 10^-6 F * (6.0 V)^2

Simplifying:
Work = 0.5 * 7.6 × 10^-6 F * 36 V^2
Work = 0.5 * 7.6 × 10^-6 F * 36
Work = 136.8 × 10^-6 J

Therefore, the work done by the battery in charging the capacitor is 136.8 microjoules.

Answer 2

The work done by the battery to charge the capacitor is equal to the electric potential energy stored in the capacitor at full charge, which is given by:

`W=U= (1)/(2)CV^2`
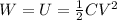
where

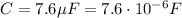
`C=7.6 \mu F=7.6 \cdot 10^(-6) F` is the capacitance of the capacitor

`V=6.0 V` is the voltage across the capacitor (which corresponds to the voltage of the battery)

By substituting the numbers into the equation, we find the work done:

`W= (1)/(2)(7.6 \cdot 10^(-6) F)(6.0 V)^2=1.37 \cdot 10^(-4)J`