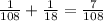Question

Ramone has 5 difficult questions left to answer on a multiple choice test.

Unfortunately, he is running out of time and must guess for the remaining questions.
Each question has 3 choices.
For the first 2 of these questions, he eliminated 1 of the 3 choices.
Find the probability that he will answer the first 2 questions, as well as at least 2 of the 3 remaining questions correctly.

Answer 1

For the first two questions, since only 2 viable choices remain, he has a
`(1)/(2)` chance on each of them. For the last 3 questions, since there are 3 choices, he has a
`(1)/(3)` chance for them.
The probability that he gets all 5 right is

`( (1)/(2))^2 ((1)/(3) )^3 = (1)/(108)`
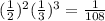
The probability that he gets one of the last 3 wrong, and everything else right, is:

`( (1)/(2))^2 ((1)/(3) )^2 ((2)/(3))*3 = (1)/(18)`
Therefore the total probability is:

`(1)/(108) + (1)/(18) = (7)/(108)`