Notice that the first interval [-3,-1) is closed at -3 but open at -1, which means that when the value of

is between -3 and -0.999... the value of

is -3; in other words the function for the first piece is:
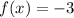
,
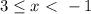
The second interval [-1,1) is closed at -1 but open at 1, which means that when the value of

is between -1 and 0.999.. the value of

is -1; in other words, the function of the second piece is:
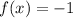
,
 We can conclude that the value of
We can conclude that the value of 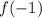 is -1.
is -1.