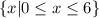Question

The table below represents the distance of a truck from its destination as a function of time:

Time Distance
(hours) (time)
x y

0 330
1 275
2 220
3 165
4 110


Part A: What is the y-intercept of the function, and what does this tell you about the truck? (4 points)

Part B: Calculate the average rate of change of the function represented by the table between x = 1 to x = 4 hours, and tell what the average rate represents. (4 points)

Part C: What would be the domain of the function if the truck continued to travel at this rate until it reached its destination? (2 points)

Answer 1

Part A: The y-intercept of the linear graph is when x=0. So, from our date, the y-intercept is at y=330

Part B: The rate of change is 55 and it represents the decrease of 55 miles for every hour travelled

Part C: The domain of the function will be meaning the traveller will reach its destination after travelling hours (assuming the traveller doesn't stop for break)

Answer 2

Part A:
The y-intercept of the function is given when x = 0. We already have a y-value for x = 0, and that y-value is 330.

Assuming miles is the unit used here for distance, this means that the truck was started 330 miles away from its destination.

Part B:
The average rate of change is represented by the slope of this function. We can find the slope of this function with the rise over run formula:


`(y_(2)-y_(1))/(x_(2)-x_(1))`

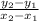
We are asked to use the points at x = 1 and x = 4. Plug the x and y values into the formula:

(1,275) and (4,110)

`(110-275)/(4-1) = (-165)/(3) = -55`

The average rate of change of the function is -55. This represents the average miles per hour the truck travels towards its destination.

Part C:
This part asks for the x-intercept of the equation. The x-intercept is defined where y = 0, which represents the destination the truck is traveling to. The domain would be restricted by the y-intercept and x-intercept, as the truck stops once it reaches its destination. We are missing the x-intercept, so we'll use the slope and the y-intercept to find it.

To find the x-intercept, we must divide the y-intercept by the slope, and subtract the result from the y-intercept's x-value:


`330 / -55 = -6`

`0 - (-6) = 6`
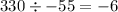
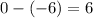The x-intercept is located at (6,0). The domain can be stated as follows:


`\x`