Question

Given that segments AE = 4 in, DE = 12 in, and EF = 8 in.

What is the measure of segment EB?

A. 6 in.
B. 16 in.
C. 24 in.
D. 4 in.

Answer 1

C is the correct answer

`4 x = 8 * 12 \\ 4x = 96 \\ x = (96)/(4) = 24`




good luck

Answer 2

To solve this question we will use the theorem which states that: "If two chords intersect in a circle, the product of the lengths of the segments of one chord equal the product of the segments of the other".

Thus, from the given diagram we will have, as per the theorem:

`AE* EB=DE* EF`

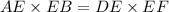
Now, the segments AE = 4 in, DE = 12 in, and EF = 8 in. as given in the question.

Therefore, substituting the values we get:

`4* EB=12* 8`

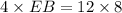
Thus,
`EB=(96)/(4)=24 in`

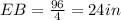
Therefore, Option C is the correct option