For this case, the first thing we must observe is that the triangles are similar.
We can then use the following relationship:
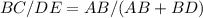
Clearing the value of BC we have:
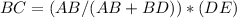
Substituting the values we have:

Rewriting we have:
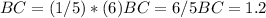 Answer:
Answer:
The length of BC is given by:
BC = 1.2