Question

ABDC is a trapezoid. Line AB = 2.5, and Line EF = 4.5. What is the length of Line CD ?

7.0
2.0
3.5
3.75

Answer 1

The correct answer is 3.5

A trapezoid is a 4-sided flat shape with straight sides. This shape has a pair of opposite sides parallel. So according to the figure we know the following:


`\overline{AC}=\overline{CE}`

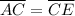
And it is also true that:


`\overline{BD}=\overline{EF}`

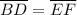
We know that the lengths of the parallel sides are given by:


`\overline{AB}=2.5 \\ \\ \overline{EF}=4.5`

So the goal is to find the length of Line CD. This line is in fact the median of the trapezoid (also called a midline or midsegment) that is a line segment half-way between the two bases and it can be found as follows:


`m=\frac{\overline{AB}+\overline{EF}}{2}=(2.5+4.5)/(2)=(7)/(2) \\ \\ \therefore \boxed{\overline{CD}=m=3.5}`

Answer 2

The line CD is the median of thre trapezoid, therefore its measures is shown below:
You must sum the largest base and the shortest base and divide both of them by 2, as following:
CD=(4.5+2.5)/2
CD=7/2
CD=3.5
Therefore, as you can see, the measure of the line CD is 3.5
The answer is: 3.5