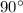Question

Do you guys know what’s the answer

Answer 1

You can see reflections everywhere. In mirror, glass, lake, river, beach, etc. So if you take a central line every point is the same distance from the central line (also called mirror line or axis of symmetry). So let's analyze each item in this problem to find what is true.

So we have the triangle ΔABC and the line of reflection
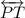
`\overleftrightarrow{PT}`, that is, the mirror line. We also know the reflected object that is ΔA'B'C', thus:

1.
`A'A=C'C`

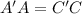
This is false. The distance from A to the mirror line is equal to the distance from this line to the point A'. On the other hands, the distance from C to the mirror line is equal the distance from this line to the point C' but it doesn't mean that necessarily A'A=C'C. You might have the point A far away from the line while the point C might be near to it, or vice versa, giving place to different distances.

2.
`C'Q=QC`

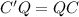
This is true. The main characteristic of reflecting shapes is that every point of it is the same distance from the central line.

3.
`\overleftrightarrow{PT} \perp \overline{A'A}`

This is true. When reflecting points, you must reflect them across the mirror line always perpendicularly. So the given segment is perpendicular to the line.

4.
`\overline{C'C}=\overline{B'B}`

This is false. In fact, this two lines are parallel.

5.
`\overline{A'A} \parallel \overline{B'B}`

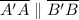
This is true given that every reflecting point is reflected across the line perpendicularly to it.

6.
`m \angle TRB=90^(\circ)`

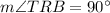
This is true. Given that the segment
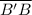`\overline{B'B}` is perpendicular to the mirror line, then this angle must be equal to
`90^(\circ)`