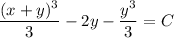Let's check if the ODE is exact. To do that, we want to show that if
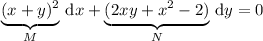
then
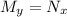
. We have
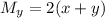
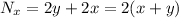
so the equation is indeed exact. We're looking for a solution of the form
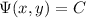
. Computing the total differential yields the original ODE,
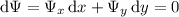

Integrate both sides of the first PDE with respect to

; then
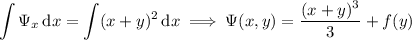
where
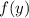
is a function of

alone. Differentiate this with respect to

so that
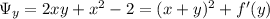
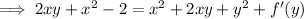

So the solution to this ODE is
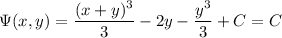
i.e.