Question

The population of a particular city is given by the function P(t) = 49,700(1.05)t, where t is time in years and P(t) is the population after t years. What is the current population, the percentage growth rate, and the population size (rounded to the nearest whole person) after 15 years?

Answer 1

The current population would be P(0), at t = 0, which is:

`P(0) = 49700(1.05)^(0) = 49700.`
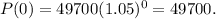
The growth rate is 5% (from 1.05). The base of the exponential term is always (1 + growth rate).
The population size after t = 15 years is P(15):

`P(15) = 49700(1.05)^(15) = 103322.73 = 103322`
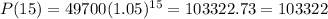
Therefore there are 103322 people after 15 years.