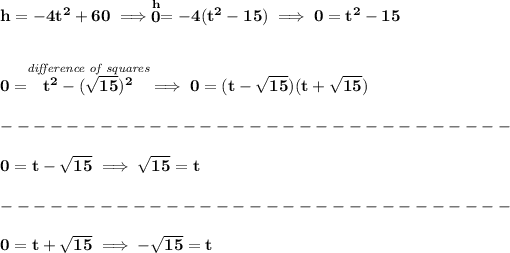Question

I need help answering a Quadratic Relation word problem.

Answer 1

check the picture below, that one use feet, but is the same thing, in this case is just centimeters.

a)

so the parabola highest point is at the vertex's y-coordinate, which one will that be?


`\bf h=-4t^2+60\implies h=-4t^2+0t+60 \\\\\\ \textit{vertex of a vertical parabola, using coefficients} \\\\ \begin{array}{lcccl} h = & -4t^2& +0t& +60\\ &\uparrow &\uparrow &\uparrow \\ &a&b&c \end{array} \qquad \left(-\cfrac{ b}{2 a}\quad ,\quad c-\cfrac{ b^2}{4 a}\right) \\\\\\ \left(~~~~~~,~~60-\cfrac{0^2}{4(-4)} \right)\implies \left(~~~~~~,~~60-0 \right)\implies (~~~~,~60)`



b)

well, when t = 3, you'll just get h = -4(3)² + 60.

and surely you know what that is.



c)

recall that the x-intercepts occur when y = 0, in this case, when h = 0,


`\bf h=-4t^2+60\implies \stackrel{h}{0}=-4(t^2-15)\implies 0=t^2-15 \\\\\\ 0=\stackrel{\textit{difference of squares}}{t^2-(√(15))^2}\implies 0=(t-√(15))(t+√(15))\\\\ -------------------------------\\\\ 0=t-√(15)\implies √(15)=t\\\\ -------------------------------\\\\ 0=t+√(15)\implies -√(15)=t`