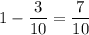Question

The figure below shows a shaded rectangle inside a large rectangle: A rectangle of length 10 units and width 5 units is shown. Inside this rectangle is another rectangle of length 9 units and width 3 units placed symmetrically inside the larger rectangle. The smaller rectangle is shaded gray. If you choose a point inside the large rectangle, what is the probability that it is not inside the shaded rectangle?

Answer 1

100/50 = x/27
50x=2700
x=54 (small rectangle is 54% of the large rectangle
100% - 54% =46% (46% is not shaded)
Probability 46% or 23/50

Answer 2

Answer:
`(7)/(10)`

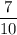
Explanation:

Given : The length of larger rectangle = 10 units

The width of larger rectangle = 5 units

The area of the larger rectangle will be :-

`A=5*10=50\text{ units}^2`

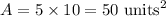
The length of smaller rectangle = 9 units

The width of the smaller rectangle = 3 units

The area of the smaller rectangle will be :-

`A=3*9=27\text{ units}^2`

Now, the probability that it is inside the shaded rectangle :-

`(27)/(90)=(3)/(10)`

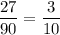
Then , the probability that it is not inside the shaded rectangle will be:-

`1-(3)/(10)=(7)/(10)`