Question

A seaplane flies horizontally over the ocean at 50 meters/second. It releases a buoy, which lands after 21 seconds. What's the vertical displacement from the plane to the ocean? (Note: Displacement will end up negative, since the direction is down.)

Answer 1

The motion of the buoy is a composition of two independent motions:
- a uniform motion on the horizontal axis, with constant speed vx=50 m/s
- an uniformly accelerated motion on the vertical axis, with constant acceleration
`g=9.81 m/s^2`

Since we want to find the vertical displacement, we are only interested in the vertical motion.
The law of motion on the vertical direction is given by:

`y(t)=h+v_(0y) t+ (1)/(2)gt^2`
where
h is the initial height of the buoy

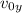
`v_(0y)` is the initial vertical velocity of the buoy, which is zero
t is the time

We know that the buoy lands after t=21 seconds, this means that the vertical position at t=21 s is y(21 s)=0. If we substitute these data into the equation, we can find the value of h, the initial height of the buoy:

`0=h+ (1)/(2)gt^2`

`h= -(1)/(2)gt^2= -(1)/(2)(9.81 m/s^2)(21 s)^2=-2163 m`
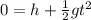
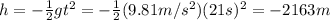
And this corresponds to the vertical displacement of the buoy.