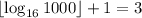Question

How many digits in hex do you need to represent integers up to 1, 000?

Answer 1

You can convert 1000 to hex and see how many digits that requires:


`1000_(10)=(3\cdot16^2+14\cdot16+8)_(10)=3\mathrm e8_(16)`

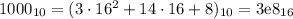
So every integer below 1000 needs up to 3 digits.

Alternatively, we know that
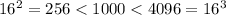
`16^2=256<1000<4096=16^3`, and that
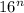
`16^n` requires
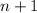
`n+1` digits in its hex representation (e.g.
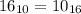
`16_(10)=10_(16)`). Taking the logarithm, we get
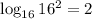
`\log_(16)16^2=2`, and adding 1 gives the number of digits needed to represent
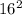
`16^2`. Similarly,



`\lfloor\log_(16)1000\rfloor+1=3`