The IVT would say that for a continuous function

on an interval
![[a,b]](https://img.qammunity.org/2019/formulas/mathematics/high-school/hycs8sttkhnuq5yfuhyfhr31suzra3n6sc.png)
, we can guarantee that for some value of
![c\in[a,b]](https://img.qammunity.org/2019/formulas/mathematics/high-school/1qzdpbpfk76td6utx7555lrqzxpzhnd62m.png)
we have
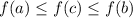
or
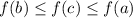
, depending on how

behaves over the given interval.
If the polynomial passes through (0, 10) and (6, -8), then we know there is some

such that
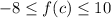
. In that case, only the second option makes sense. We can't claim to know anything about how

behaves between values of 0 and 6, only between the values of -8 and 10, so we ignore the first and third options. The fourth scenario is possible, but not something we can guarantee because the IVT doesn't make claims about what is not possible.