Answer with explanation:
The given series is

The given series is a geometric sequence,whose common ratio is equal to
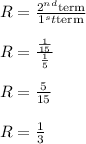
Sum to Infinity is given by the formula

As the sum of series is Finite, that is having a single value, so the series is Convergent.
If it has more than one sum, it would have been Divergent.
Option D: It converges; it has a sum.