Question

Need professional help for this problem

Answer 1

keeping in mind that, the diameter of A is 24, thus its radius is 12, and B's diameter is 22, thus its radius is 11.


`\bf \textit{volume of a cylinder}\\\\ V=\pi r^2 h\qquad \qquad \qquad \qquad \begin{array}{llll} \stackrel{\textit{volume of cylinder A}}{\pi(12^2)(18) }\implies 2592\pi \\\\\\ \stackrel{\textit{volume of cylinder B}}{\pi(11^2)(20) }\implies 2420\pi \end{array}`

how much is left? well 2592π - 2420π, that much.

Answer 2

Container A is completely full while container B has nothing in it.

When container B is completely full after the pumping, the volume of water left in container A will be equivalent to the volume of container A subtracted by the volume of container B.

The volume of any right cylinder is
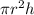
`\pi r^2 h` where r is the radius and h is the height of the cylinder.

The diameters of the cylinders are given. The radius is half of the diameters.
The radius of container A is 24/2, or 12. The radius of container B is 22/2, or 11.


`\text{Volume of Container A}= \pi r^2 h = \pi * 12^2 * 18`

`\approx 8138.88`


`\text{Volume of Container B}= \pi r^2 h = \pi * 11^2 * 20`

`\approx 7598.8`

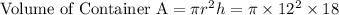
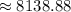
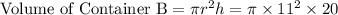
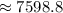
Now, subtract the two volumes.


`\text{Volume of Container A} - \text{Volume of Container B} = 540.08`

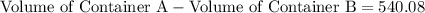
Rounding this to the nearest tenth of a cubic foot will give 540.1 cubic feet. Thus, container A will have approximately 540.1 cubic feet of water after container B is completely full.