Question

Find the angle B in an oblique triangle in which a = 31, b = 15, and c = 17. A. 13º28' B. 15º19' C. 151º13' D. 148º47'

Answer 1

Hello,
Please, see the attached file.
Thanks.

Answer 2

We can find the measure of angle B using the Law of cosines.

According to the Law of Cosines:


`b^(2) = a^(2) + c^(2) - 2ac*cos(B) \\ \\ 2ac*cos(B)= a^(2) + c^(2)- b^(2) \\ \\ cos(B)= (a^(2) + c^(2)- b^(2))/(2ac)`

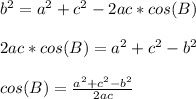
Using the values of a,b and c in the above equation we get:


`cos(B)= (31^(2)+17^(2)-15^(2))/(2*31*17) \\ \\ cos(B)= (1025)/(1054) \\ \\ B=cos^(-1)((1025)/(1054)) \\ \\ B=13.47`

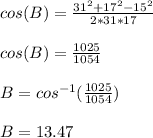
Thus measure of angle B is 13.47 degrees. We can convert the decimal part to minutes by multiplying it by 60.

So measure of angle B will be 13 degrees and (60 x 0.47) minutes which equals 13 degrees and 28 minutes or 13° 28'.

Thus option A gives the correct answer.