Question

Interest rate 8% How long will it take for a $2000 investment to double in value? What will be the value in seven years of $12,000 invested today? How much would you pay for the right to receive $5000 at the end of year one, $4000 at the end of year two and $8000 at the end of year five?

Answer 1

for a Principal of $2000 to double up, it will be $4000, so with a rate of 8%, when is that?


`\bf ~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\to &\$4000\\ P=\textit{original amount deposited}\to& \$2000\\ r=rate\to 8\%\to (8)/(100)\to &0.08\\ t=years \end{cases} \\\\\\ 4000=2000(1+0.08t)\implies \cfrac{4000}{2000}=1+0.08t\implies 2=1+0.08t \\\\\\ 1=0.08t\implies \cfrac{1}{0.08}=t\implies 12.5=t`



$12000 at 8% rate for 7years with simple interest?


`\bf ~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\to& \$12000\\ r=rate\to 8\%\to (8)/(100)\to &0.08\\ t=years\to &7 \end{cases} \\\\\\ A=12000(1+0.08\cdot 7)\implies A=18720`



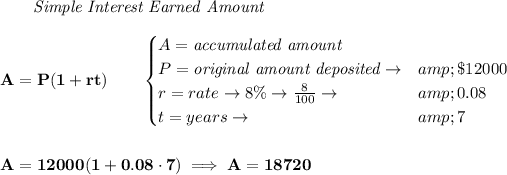
now, for these ones, we'll assume the interest is still 8%, simple interest, and is asking for the Principal, how much would you put in in order to get $5000 for 1 year.


`\bf ~~~~~~ \textit{Simple Interest Earned} \\\\ I = Prt\qquad \begin{cases} I=\textit{interest earned}\to &\$5000\\ P=\textit{original amount deposited}\\ r=rate\to 8\%\to (8)/(100)\to &0.08\\ t=years\to &1 \end{cases} \\\\\\ 5000=P(0.08)(1)\implies \cfrac{5000}{(0.08)(1)}=P\implies 62500=P`



how about for for $4000 at 8% for 2 years?


`\bf ~~~~~~ \textit{Simple Interest Earned} \\\\ I = Prt\qquad \begin{cases} I=\textit{interest earned}\to &\$4000\\ P=\textit{original amount deposited}\\ r=rate\to 8\%\to (8)/(100)\to &0.08\\ t=years\to &2 \end{cases} \\\\\\ 4000=P(0.08)(2)\implies \cfrac{4000}{(0.08)(2)}=P\implies 25000=P`



how about for $8000 at 8% for 5 years?


`\bf ~~~~~~ \textit{Simple Interest Earned} \\\\ I = Prt\qquad \begin{cases} I=\textit{interest earned}\to &\$8000\\ P=\textit{original amount deposited}\\ r=rate\to 8\%\to (8)/(100)\to &0.08\\ t=years\to &5 \end{cases} \\\\\\ 8000=P(0.08)(5)\implies \cfrac{8000}{(0.08)(5)}=P\implies 20000=P`